ภูมิศักดิ์ โคตรสมบัติ: วิชาคณิตศาสตร์

ลิงก์ข้ามภาษาในบทความนี้ มีไว้ให้ผู้อ่านและผู้ร่วมแก้ไขบทความศึกษาเพิ่มเติมโดยสะดวก เนื่องจากวิกิพีเดียภาษาไทยยังไม่มีบทความดังกล่าว กระนั้น ควรรีบสร้างเป็นบทความโดยเร็วที่สุด

บทความนี้ได้รับแจ้งให้ปรับปรุงตามด้านล่าง กรุณาช่วยปรับปรุงบทความ หรือเสนอแนะที่หน้าอภิปราย

บทความนี้ต้องการจัดรูปแบบข้อความ การจัดหน้า การแบ่งหัวข้อ การจัดลิงก์ภายใน และอื่น ๆ
บทความนี้ยังขาดแหล่งอ้างอิง

เว็บย่อ: math

ยูคลิด นักคณิตศาสตร์ชาวกรีก ในสมัย 300 ปีก่อนคริสตกาล ภาพวาดของราฟาเอลในชื่อโรงเรียนแห่งเอเธนส์

ในอดีตผู้คนจะใช้สิ่งของแทนจำนวนที่จะนับยิ่งนานเข้าจำนวนประชากรยิ่งมี มากขึ้น ทำให้ผู้คนเริ่มคิดที่จะประดิษฐ์ตัวเลขขึ้นมาแทนการนับที่ใช้สิ่งของนับแทน จากนั้นก็มีการบวก ลบคูณ และหาร จากนั้นก็ก่อให้เกิดคณิตศาสตร์ คณิตศาสตร์ เป็นศาสตร์ที่มุ่งค้นคว้าเกี่ยวกับ โครงสร้างนามธรรมที่ถูกกำหนดขึ้นผ่านทางกลุ่มของสัจพจน์ซึ่งมีการให้เหตุผลที่แน่นอนโดยใช้ตรรกศาสตร์สัญลักษณ์ และสัญกรณ์คณิตศาสตร์ เรามักนิยามโดยทั่วไปว่าคณิตศาสตร์เป็นสาขาวิชาที่ศึกษาเกี่ยวกับรูปแบบและโครงสร้าง, การเปลี่ยนแปลง, และปริภูมิ กล่าวคร่าว ๆ ได้ว่าคณิตศาสตร์นั้นสนใจ "รูปร่างและจำนวน" เนื่องจากคณิตศาสตร์มิได้สร้างความรู้ผ่านกระบวนการทดลอง บางคนจึงไม่จัดว่าคณิตศาสตร์เป็นสาขาของวิทยาศาสตร์
คำว่า "คณิตศาสตร์" (คำอ่าน: คะ-นิด-ตะ-สาด) มาจากคำว่า คณิต (การนับ หรือ คำนวณ) และ ศาสตร์ (ความรู้ หรือ การศึกษา) ซึ่งรวมกันมีความหมายโดยทั่วไปว่า การศึกษาเกี่ยวกับการคำนวณ หรือ วิชาที่เกี่ยวกับการคำนวณ. คำนี้ตรงกับคำภาษาอังกฤษว่า mathematics มาจากคำภาษากรีก μάθημα (máthema) แปลว่า "วิทยาศาสตร์, ความรู้, และการเรียน" และคำว่า μαθηματικός (mathematikós) แปลว่า "รักที่จะเรียนรู้". ในอเมริกาเหนือนิยมย่อ mathematics ว่า math ส่วนประเทศอื่น ๆ ที่ใช้ภาษาอังกฤษนิยมย่อว่า maths
ความรู้ทางด้านคณิตศาสตร์เพิ่มขึ้นอย่างสม่ำเสมอ ผ่านทางการวิจัยและการประยุกต์ใช้ คณิตศาสตร์เป็นเครื่องมืออันหนึ่งของวิทยาศาสตร์ อย่างไรก็ตาม การคิดค้นทางคณิตศาสตร์ไม่จำเป็นต้องมีเป้าหมายอยู่ที่การนำไปใช้ทางวิทยา ศาสตร์ (ดู คณิตศาสตร์บริสุทธิ์ และคณิตศาสตร์ประยุกต์)
โครงสร้างต่าง ๆ ที่นักคณิตศาสตร์สนใจและพิจารณานั้น มักจะมีต้นกำเนิดจากวิทยาศาสตร์ธรรมชาติ และสังคมศาสตร์ โดยเฉพาะฟิสิกส์ และเศรษฐศาสตร์. ปัญหาทางคณิตศาสตร์ในปัจจุบัน ยังเกี่ยวข้องกับการประยุกต์ใช้ในสาขาวิทยาการคอมพิวเตอร์ และทฤษฎีการสื่อสาร อีกด้วย
เนื่องจากคณิตศาสตร์นั้นใช้ตรรกศาสตร์สัญลักษณ์และสัญกรณ์คณิตศาสตร์ ซึ่งทำให้กิจกรรมทุกอย่างกระทำผ่านทางขั้นตอนที่ชัดเจน เราจึงสามารถพิจารณาคณิตศาสตร์ว่า เป็นระบบภาษาที่เพิ่มความแม่นยำและชัดเจนให้กับภาษาธรรมชาติ ผ่านทางศัพท์และไวยากรณ์บางอย่าง สำหรับการอธิบายและศึกษาความสัมพันธ์ทั้งทางกายภาพและนามธรรม. ความหมายของคณิตศาสตร์นั้นยังมีอีกหลายมุมมอง ซึ่งหลายอันถูกกล่าวถึงในบทความเกี่ยวกับปรัชญาของคณิตศาสตร์
คณิตศาสตร์ยังถูกจัดว่าเป็นศาสตร์สัมบูรณ์ โดยจำไม่เป็นต้องมีการอ้างถึงใด ๆ จากโลกภายนอก. นักคณิตศาสตร์กำหนด และพิจารณาโครงสร้างบางประเภท สำหรับใช้ในคณิตศาสตร์เองโดยเฉพาะ, เนื่องจากโครงสร้างเหล่านี้ อาจทำให้สามารถอธิบายสาขาย่อย ๆ หลาย ๆ สาขาได้ในภาพรวม หรือเป็นประโยชน์ในการคำนวณพื้นฐาน
นอกจากนี้ นักคณิตศาสตร์หลายคนก็ทำงานเพื่อเป้าหมายเชิงสุนทรียภาพเท่านั้น โดยมองว่าคณิตศาสตร์เป็นศาสตร์เชิงศิลปะ มากกว่าที่จะเป็นศาสตร์เพื่อการนำไปประยุกต์ใช้ (ดังเช่น จี. เอช. ฮาร์ดี ที่ได้กล่าวไว้ในหนังสือ A Mathematician's Apology) ; แรงผลักดันในการทำงานเช่นนี้ มีลักษณะไม่ต่างไปจากที่กวีและนักปรัชญาได้ประสบ และเป็นสิ่งที่ไม่สามารถอธิบายได้. อัลเบิร์ต ไอน์สไตน์ กล่าวว่า คณิตศาสตร์เป็นราชินีของวิทยาศาสตร์ ในหนังสือ Ideas and Opinions ของเขา
องค์ความรู้ในคณิตศาสตร์รวมกันเป็นสาขาวิชา หลักการเบื้องต้นที่เริ่มจากเลขคณิตไปยังการประยุกต์ใช้งานพื้นฐานของสาขาคณิตศาสตร์ ที่รวมพีชคณิต เรขาคณิต ตรีโกณมิติ สถิติศาสตร์ และแคลคูลัส เป็นหลักสูตรแกนใน การศึกษาขั้นพื้นฐาน แม้ว่าจะได้มีการพัฒนาและขยายขอบเขตไปอย่างมากมายในช่วงเวลาหลายร้อยปี สาขาวิชาคณิตศาสตร์ยังคงถูกจัดว่าเป็นสาขาวิชาเดี่ยว ที่มีลักษณะแตกต่างจากสาขาอื่น ๆ

เนื้อหา

ประวัติ

พัฒนาการ

นักคณิตศาสตร์กรีกพีทาโกรัส (ค.ศ. 570 - ค.ศ. 495 ก่อนคริสต์ศักราช) ได้รับการยกย่องในเรื่องที่เกี่ยวข้องกับการค้นพบทฤษฎีบทพีทาโกรัส (Pythagorean theorem)

วิวัฒนาการของคณิตศาสตร์อาจถูกมองว่าเป็นชุดของการเพิ่มขึ้นของภาวะนามธรรมหรืออาจเป็นการขยายตัวของวิชาที่เกี่ยวกับสสาร ภาวะนามธรรมที่เกิดขึ้นเป็นครั้งแรกนั้น, มีส่วนเกี่ยวข้องกับสัตว์หลาย ๆ ชนิด, ^[1] เป็นความน่าจะเป็นที่เกี่ยวข้องกับจำนวน

หัวข้อทางคณิตศาสตร์

รายการด้านล่างนี้ แสดงลักษณะหนึ่งของการแบ่งย่อยของหัวข้อทางคณิตศาสตร์เท่านั้น สำหรับการแบ่งหัวข้อตาม 2000 Mathematics Subject Classification (MSC2000) ดู: สาขาของคณิตศาสตร์

ปริมาณ

โดยทั่วไป หัวข้อและแนวคิดเหล่านี้เกี่ยวข้องกับการวัดขนาดของตัวเลข หรือเซต หรือว่าวิธีการวัดค่าดังกล่าว

$1, 2, 3\, \!$	$-2, -1, 0, 1, 2\, \!$	$-2, \frac{2}{3}, 1.21\, \!$	$-e, \sqrt{2}, 3, \pi\, \!$	$2, i, -2+3i, 2e^{i\frac{4\pi}{3}}\, \!$
จำนวนธรรมชาติ	จำนวนเต็ม	จำนวนตรรกยะ	จำนวนจริง	จำนวนเชิงซ้อน

จำนวน - จำนวนธรรมชาติ - จำนวนเต็ม - จำนวนตรรกยะ - จำนวนจริง - จำนวนเชิงซ้อน - จำนวนเชิงพีชคณิต - ควอเทอร์เนียน - ออคโทเนียน (Octonions) - จำนวนเชิงอันดับที่ (ordinal number) - จำนวนเชิงการนับ - ลำดับของจำนวนเต็ม - ค่าคงที่ทางคณิตศาสตร์ - อนันต์

โครงสร้าง

สาขาเหล่านี้ ศึกษาขนาดและความสมมาตรของจำนวนและวัตถุทางคณิตศาสตร์ต่าง ๆ


ทฤษฎีจำนวน	พีชคณิตนามธรรม	ทฤษฎีกรุป	ทฤษฎีลำดับ

พีชคณิตนามธรรม - ทฤษฎีจำนวน - ทฤษฎีกรุป - ทอพอโลยี - พีชคณิตเชิงเส้น - ทฤษฎีประเภท (Category theory) - ทฤษฎีลำดับ (Order theory)

ความสัมพันธ์เชิงปริภูมิ

สาขาเหล่านี้ มักใช้วิธีการเชิงรูปภาพมากกว่าในสาขาอื่น ๆ


เรขาคณิต	ตรีโกณมิติ	เรขาคณิตเชิงอนุพันธ์	ทอพอโลยี	เรขาคณิตสาทิสรูป

ทอพอลอยี - เรขาคณิต - ตรีโกณมิติ - เรขาคณิตเชิงพีชคณิต - เรขาคณิตเชิงอนุพันธ์ - ทอพอโลยีเชิงอนุพันธ์ - ทอพอโลยีเชิงพีชคณิต - พีชคณิตเชิงเส้น - เรขาคณิตสาทิสรูป

ความเปลี่ยนแปลง

หัวข้อเหล่านี้ เกี่ยวข้องกับการวัดความเปลี่ยนแปลงของฟังก์ชันทางคณิตศาสตร์ และความเปลี่ยนแปลงระหว่างจำนวน


แคลคูลัส	แคลคูลัสเวกเตอร์	สมการเชิงอนุพันธ์	ระบบพลวัติ	ทฤษฎีความอลวน

เลขคณิต - แคลคูลัส - แคลคูลัสเวกเตอร์ - คณิตวิเคราะห์ - ทฤษฎีการวัด - การวิเคราะห์เชิงฟังก์ชัน - การวิเคราะห์เชิงจินตภาพ - การวิเคราะห์ฟูร์ริเยร์ - สมการเชิงอนุพันธ์ - ระบบพลวัติ - ทฤษฎีความอลวน - รายการฟังก์ชัน

พื้นฐานและวิธีการ

หัวข้อเหล่านี้คือแนวทางการเข้าถึงคณิตศาสตร์และมีอิทธิพลต่อวิธีที่นักคณิตศาสตร์ใช้ในการศึกษา

$p \Rightarrow q \,$
ตรรกศาสตร์	ทฤษฎีเซต	ทฤษฎีประเภท

ปรัชญาคณิตศาสตร์ - พื้นฐานคณิตศาสตร์ (Foundations of mathematics) - ทฤษฎีเซต - ตรรกศาสตร์สัญลักษณ์ - ทฤษฎีโมเดล - ทฤษฎีประเภท - ตรรกศาสตร์

วิยุตคณิต

วิยุตคณิต คือแขนงของคณิตศาสตร์ที่สนใจวัตถุที่มีค่าเฉพาะเจาะจงที่แตกต่างกัน

$\begin{matrix} (1, 2, 3) & (1, 3, 2) \\ (2, 1, 3) & (2, 3, 1) \\ (3, 1, 2) & (3, 2, 1) \end{matrix}$
คณิตศาสตร์เชิงการจัด	ทฤษฎีการคำนวณ	วิทยาการเข้ารหัสลับ	ทฤษฎีกราฟ

คณิตศาสตร์เชิงการจัด - ทฤษฎีการคำนวณ - วิทยาการเข้ารหัสลับ - ทฤษฎีกราฟ

คณิตศาสตร์ประยุกต์

สาขาในคณิตศาสตร์ประยุกต์ ใช้ความรู้ทางคณิตศาสตร์เพื่อแก้ปัญหาในโลกของความเป็นจริง

คณิตศาสตร์ฟิสิกส์ - กลศาสตร์ - กลศาสตร์ของไหล - การวิเคราะห์เชิงตัวเลข - การหาค่าเหมาะที่สุด (Optimization) - ความน่าจะเป็น - สถิติศาสตร์ - คณิตศาสตร์การเงิน - ทฤษฎีเกม - คณิตชีววิทยา (Mathematical biology) - วิทยาการเข้ารหัสลับ - ทฤษฎีข้อมูล - ทฤษฎีระบบควบคุม

ทฤษฎีบทที่สำคัญ

ทฤษฎีบทเหล่านี้ เป็นที่สนใจของทั้งนักคณิตศาสตร์และบุคคลทั่วไป

ข้อความคาดการณ์ที่สำคัญ

ปัญหาคณิตศาสตร์ที่ยังไม่มีใครแก้ได้

ข้อความคาดการณ์ของโกลด์บาช - ข้อความคาดการณ์จำนวนเฉพาะคู่แฝด - สมมติฐานของรีมันน์ - สมมติฐานความต่อเนื่อง - ข้อความคาดการณ์ของปวงกาเร - P=NP? - ปัญหาของฮิลแบร์ท

ประวัติและโลกของนักคณิตศาสตร์

ประวัติของคณิตศาสตร์ - เส้นเวลาของคณิตศาสตร์ - นักคณิตศาสตร์ - เหรียญฟิลด์ส (Fields Medal) - รางวัลอาเบล (Abel Prize) - ปัญหารางวัลสหัสวรรษ (รางวัลเคลย์แมท) (Millennium Prize Problems (Clay Math Prize)) - สหภาพคณิตศาสตร์นานาชาติ (International Mathematical Union) - การแข่งขันคณิตศาสตร์ - การคิดเชิงข้าง (Lateral thinking) - ประเด็นเกี่ยวกับความสามารถทางคณิตศาสตร์และเพศ (Mathematical abilities and gender issues)

เครื่องมือทางคณิตศาสตร์

อ้างอิง

S. Dehaene; G. Dehaene-Lambertz; L. Cohen (Aug 1998). "Abstract representations of numbers in the animal and human brain". Trends in Neuroscience 21 (8): 355–361. doi:10.1016/S0166-2236 (98) 01263-6 Check |doi= value (help). PMID 9720604.

ดูเพิ่ม

สถานีย่อย:คณิตศาสตร์

เส้นเวลาของคณิตศาสตร์

แหล่งข้อมูลอื่น

คอมมอนส์ มีภาพและสื่อเกี่ยวกับ:
Mathematics

ภาษาไทย

คณิตศาสตร์เบื้องต้น จากสารานุกรมสำหรับเยาวชน
แหล่งรวมความรู้ด้านคณิตศาสตร์ จากเครือข่ายคอมพิวเตอร์เพื่อโรงเรียนไทย

ภาษาอื่น

สารานุกรมคณิตศาสตร์ (อังกฤษ)
The Mathematical Atlas - แนะนำสาขาต่าง ๆ ของคณิตศาสตร์สมัยใหม่
Planet Math^{[ลิงก์เสีย]} - สารานุกรมคณิตศาสตร์ เน้นคณิตศาสตร์สมัยใหม่
MathWorld - สารานุกรมคณิตศาสตร์ เน้นคณิตศาสตร์ดั้งเดิม
Metamath - อธิบาย และพิสูจน์หลักการทางคณิตศาสตร์ต่าง ๆ อย่างเป็นขั้นเป็นตอน
Interactive Mathematics Miscellany and Puzzles - บทความ และเกมคณิตศาสตร์ เล่นออนไลน์ได้

ชุมชนไทย

ศูนย์กลางคณิตศาสตร์ไทย - เว็บไซต์สำหรับผู้มีใจรักคณิตศาสตร์
เครื่องคิดเลข - เว็บไซต์สำหรับคำนวณเกี่ยวกับคณิตศาสตร์

[ซ่อน]

สาขาที่สำคัญของคณิตศาสตร์

ตรรกะ · ทฤษฎีเซต · คณิตศาสตร์เชิงการจัด · พีชคณิต (พื้นฐาน – เชิงเส้น – นามธรรม) · วิยุตคณิต · ทฤษฎีจำนวน · คณิตวิเคราะห์ · เรขาคณิต · ทอพอโลยี · คณิตศาสตร์ประยุกต์ · ความน่าจะเป็น · สถิติศาสตร์ · คณิตศาสตร์ฟิสิกส์

หมวดหมู่:

คณิตศาสตร์

ภูมิศักดิ์ โคตรสมบัติ

วันพุธที่ 22 กรกฎาคม พ.ศ. 2558

วิชาคณิตศาสตร์

เนื้อหา

ประวัติ

พัฒนาการ

หัวข้อทางคณิตศาสตร์

ปริมาณ

โครงสร้าง

ความสัมพันธ์เชิงปริภูมิ

ความเปลี่ยนแปลง

พื้นฐานและวิธีการ

วิยุตคณิต

คณิตศาสตร์ประยุกต์

ทฤษฎีบทที่สำคัญ

ข้อความคาดการณ์ที่สำคัญ

ประวัติและโลกของนักคณิตศาสตร์

เครื่องมือทางคณิตศาสตร์

อ้างอิง

ดูเพิ่ม

แหล่งข้อมูลอื่น

ภาษาไทย

ภาษาอื่น

ชุมชนไทย

รายการเลือกการนำทาง

มีส่วนร่วม

เครื่องมือ

พิมพ์/ส่งออก

ภาษาอื่น

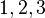
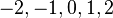
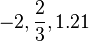
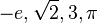
ไม่มีความคิดเห็น:

แสดงความคิดเห็น